| 語言 : |
|
| 百科社區 |百科問答 |提交問題 |詞彙知識 |上傳知識 |
 | 不可能事件
數學概念 不可能事件 : bù kě néng shì jiàn 概率論中把在一定條件下不可能發生的事件叫不可能事件。 人們通常用0來表示不可能事件發生的可能性。即:不可能事件的概率為0。 但概率為0的事件不一定為不可能事件。 延伸 一般地,我們把在條件s下,一定會發生的事件,叫做相對於事件s的必然事... | |||||||
 | 先驗概率
概述 先驗概率(prior probability)是指根據以往經驗和分析得到的概率,如全概率公式,它往往作為"由因求果"問題中的"因"出現. 先驗概率的分類 利用過去歷史資料計算得到的先驗概率,稱為客觀先驗概率; 當歷史資料無從取得或資料... | |||||||
 | 變異係數
定義 變異係數是級差、標準差和方差一樣都是反映數據離散程度的絕對值,其數據大小不僅受變量值離散程度的影響,而且還受變量值平均水平大小的影響。一般來說,變量值平均水平高,其離散程度的測度值也大,反之越小。 [1] 變異係數是衡量資料中各觀測值變異程度的另一個統計量。當進行兩個或多個資料變異程度的比較時,如果度量單位與... | |||||||
 | 中心矩
在數學的概率領域中有一類數字特徵叫矩。 (X^k為X的k次方) 中心矩:對於正整數k,如果EX存在,且E(|X - EX|^k)<∞,則稱E[X-EX]^k為隨機變量X的k階中心矩。如X的方差是X的二階中心矩,即D(X)=E{[XE(X)]^2} .... | |||||||
 | 條件期望
條件期望,又稱條件數學期望。為了方便起見,我們討論兩個隨機變量ξ 與η 的場合,假定它們具有密度函數p(x,y) ,並以p(y∣x) 記已知ξ = x 的條件下,η 的條件密度函數,以p1(x) 記ξ 的密度函數。定義在ξ = x 的條件下, η的條件數學期望定義為:E{η∣ξ = x }=∫yf(y∣x)dy。 條... | |||||||
 | 鞅
鞅,指去了毛的獸皮,就是指套在馬頸或馬腹上的皮帶。泛指牲口拉車時的器具。另外通“怏”,不愉快、煩悶的樣子。 漢字釋義 基本信息 拼音 : yāng 注音 :ㄧㄤˋ 漢字結構:左右結構 簡體部首:革 筆劃數:14 鄭碼:EELG UniCode:U 9785 GB... | |||||||
 | 平衡態
平衡態,是指系統的這樣一種狀態,即在沒有外界(指與系統有關的周圍環境)影響的條件下,系統各部分的宏觀性質長時間內不發生變化的狀態。這裡所說的沒有外界影響,是指系統與外界之間不通過作功或傳熱的方式交換能量,否則係統就不能達到並保持平衡態。由於實際中並不存在完全不受外界影響,並且宏觀性質絕對保持不變的系統,所以平衡態只是一... | |||||||
 | 伊藤過程
控制論的發明人維納在1923年指出,布朗運動在數學上是一個隨機過程,提出了用“隨機微分方程”來描述,因此人們也把布朗運動稱為維納過程;日本數學家伊藤發展建立了帶有布朗運動干擾項的隨機微分方程, dx(t)=μ(t,x)dt σ(t,x)dz σ(t,x)是乾擾強度,μ(t,x)是漂移率,σ(t,x)dz服從正態分佈... | |||||||
 | 新息
地名 古縣名。春秋息國,在今河南息縣西南。漢置縣。治所移今河南息縣,改名新息。晉為汝南郡治所。南朝宋分置南北二縣:南新息治所在原新息縣,先後為汝南郡及東西豫州、淮州治所。北新息治所在今河南息縣東,北齊時併入南新息,復名新息。蒙古至元三年(1266年)廢入息州。 數理統計 考察時間序列{x(t)},根據歷史數據對x... | |||||||
 | 組限
在進行組距式分組時,組距兩端的數值稱為組限(class boundary)。其中,每組的起點值稱為下限。連續型變量中,上一組的上限同時也是下一組的下限。在分組時,凡遇到單位的標誌值剛好等於相鄰兩組上下限數值時,一般把此值歸併到作為下限的那一組。 上限(upper boundary) 與下限(lower boundar... | |||||||
 | 子樣本
子樣本的定義 定義1:  這兩套或兩套以上的樣本,就構成“交叉樣本”,每一套樣本稱為“子樣本”.交叉樣本法每套子樣本可分派一個調查員或調查組同時調查,能大大縮短調查時間.每個子樣本指標可以獨立作為總體指標的估計值,也可以綜合起來估計總體指標 源自: 交叉樣本法在控制調查誤... | |||||||
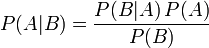 | 經驗貝葉斯方法
貝葉斯定理 貝葉斯定理是關於隨機事件A和B的條件概率和邊緣概率的一則定理。 其中P(A|B)是在B發生的情況下A發生的可能性。 在貝葉斯定理中,每個名詞都有約定俗成的名稱: P(A)是A的先驗概率或邊緣概率。之所以稱為"先驗"是因為它... | |||||||
 | 第二類錯誤
error of the second kind 為在進行假設檢驗時,原假設不正確而接受原假設的錯誤。 由於檢驗統計量是隨機變量,有一定的波動性,有時原假設H0並不正確,在正常的情況下,計算的統計量仍有一定的概率β落入接受域內,從而錯誤地接受了原假設H0。 β是限制犯第二類錯誤的保證,又稱為檢驗的污染。... | |||||||
 | 廣義線性模型
圖書信息 《廣義線性模型》 作者:喬治·H.鄧特曼(作者), 等(作者, 譯者), 林毓玲(譯者) 出版社: 格致出版社; 第1版(2011年9月4日) 叢書名: 格致方法·定量研究系列 平裝: 380頁 正文語種: 簡體中文 開本: 16 ISBN: 75432... | |||||||
 | 多重共線性
1.多重共線性的概念 所謂多重共線性(Multicollinearity)是指線性回歸模型中的解釋變量之間由於存在精確相關關係或高度相關關係而使模型估計失真或難以估計準確。一般來說,由於經濟數據的限制使得模型設計不當,導致設計矩陣中解釋變量間存在普遍的相關關係。 完全共線性的情況並不多見,一般出現的是在一定程度上的... | |||||||
 | 不放回抽樣
以從一個口袋中取球為例,每次隨機地取一隻,每次取一隻球後放回袋中,攪勻後再取一球,這種取球方式為放回取樣。 每次取一隻球後不放回袋中,下一次從剩餘的球中再取一球,這種取球方式為不放回取樣。 放回抽樣的每次抽樣過程中每個小球被抽到的機率是相等的。... | |||||||
 | 均勻設計
均勻設計(Uniform Design),又稱均勻設計試驗法(Uniform Design Experimentation)),或空間填充設計,是一種試驗設計方法(Experimental Design Method。它是只考慮試驗點在試驗範圍內均勻散佈的一種試驗設計方法。它由方開泰教授和數學家王元在1978年共同提出... | |||||||
 | 符號計算
符號計算的定義 符號計算又稱計算機代數,通俗地說就是用計算機推導數學公式,如對錶達式進行因式分解、化簡、微分、積分、解代數方程、求解常微分方程等。 符號計算與數值計算 眾所周知,科學計算包括數值計算和符號計算兩種計算。計算機能夠對數值進行一系列運算是人所共知的事,但計算機也能夠對含未知量的式子直接進行推導、演算則... | |||||||
 | 截斷誤差
由於實際運算只能完成有限項或有限步運算,因此要將有些需用極限或無窮過程進行的運算有限化,對無窮過程進行截斷,這樣產生的誤差成為截斷誤差。 例如:求一個級數的和或無窮序列的極限時,我們取有限項作為它們的近似,從而產生了誤差,這種誤差稱為截斷誤差。... | |||||||
 | 有效位數
對沒有小數位且以若干個零結尾的數值,從非零數字最左一位向右數得到的位數減去無效零的個數;對其他十進位的數,從非零數字最左一位向右數而得到的位數就是有效位數. 有效數字:一般地,一個近似數,四捨五入到哪一位,就說這個數精確到哪一位,這時,從左邊第一個不是0的數字起,到精確的數位止,所有的數字,都叫做這個數的有效數字. ... | |||||||